Wie die Spieltheorie den Bau der Atombombe erklärt

Wie kann man erklären, dass zwei Weltmächte, wie etwa die USA und die damalige Sowjetunion, gleichzeitig die Atombombe entwickeln? Wie kommt es dazu, dass man davon ausgehen muss, dass im Radsport flächendeckend gedopt wird? Antworten auf diese und weitere Fragen kann das Gefangenendilemma-Spiel geben.

Das Gefangenendilemma ist ein Standardspiel der Spieltheorie. Bei diesem handelt es sich, anders als beim Diktator-und Ultimatumspiel, um ein simultanes Spiel. Man bezeichnet es als simultan, da beide Spieler gleichzeitig ihre Entscheidung treffen. Diktator-und Ultimatumspiel gehören dagegen  zu den sequentiellen Spielen.

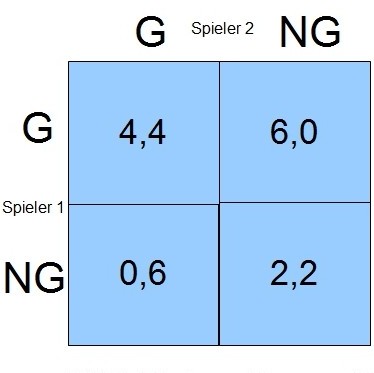
Das klassische Gefangenendilemma beschreibt folgende Situation: Zwei Straftäter werden von der Polizei verhaftet und in getrennte Zellen gesperrt (dies ist deshalb wichtig, damit sich die Gefangenen nicht absprechen können, also unabhängige Entscheidungen treffen). Nun ergibt sich die folgende Situation: Gesteht einer der beiden Straftäter und der andere gesteht die Tat nicht, wandert der Nicht-Gestehende für 6 Jahre hinter Gitter. und der Gestehende wird im Rahmen einer Kronzeugenregelung freigesprochen. Gestehen beide, so wandern sie jeweils für 4 Jahre hinter Gitter. Für den Fall jedoch, dass weder der Eine, noch der Andere gesteht, werden beide, etwa in einem Indizienprozess, nur zu 2 Jahren Haft verurteilt.

Das aus Sicht beider Spieler optimale Verhalten führt nicht zum besten Ergebnis

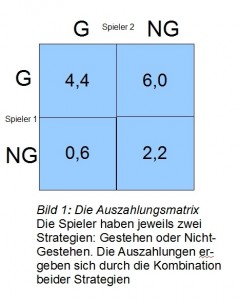In diesem Spiel ist es für beide Spieler, unabhängig von der Strategie des anderen Spielers, besser zu gestehen. Man spricht hier von (G)estehen als dominanter Strategie für beide Spieler. Aufgrund dieser dominanten Strategie werden also beide Gefangenen, wenn sie rational sind, gestehen und wandern für jeweils vier Jahre ,,in den Bau”. Es wäre jedoch  für beide Spieler besser, wenn sie kollektiv nicht gestehen würden, denn dann müssten Beide für nur zwei Jahre ins Gefängnis.

Wir haben in diesem Spiel also eine Situation, in der die beiden Spielpartner eine für Beide bessere Lösung nicht erreichen können. Dieses Spiel lässt sich auf die anfangs aufgeführten Bereiche übertragen: Wenn die USA davon ausgehen, dass die (damalige) Sowjetunion eine Atombombe baut, dann stellen sie sich besser wenn sie diese ebenfalls entwickeln. Auch wenn die Sowjets keine Atombombe bauen, stellen sie sich besser, wenn sie den Bau der Atombombe erforschen. Dieselbe Kalkulation wird von den Sowjets durchgeführt und deshalb bauen beide Mächte eine Atombombe. Diese Situation ist jedoch im Vergleich zu der Situation, in der beide Länder keine Atombombe haben, suboptimal. Jedoch lässt sich dieses Ergebnis, in dem beide Weltmächte keine Atombombe bauen, nicht erzielen.

Analog kann man das Gefangenendilemma auf den Radsport und sein Dopingproblem übertragen. Für jeden Radrennfahrer ist es in jedem Fall besser, zu dopen, unabhängig davon, ob die Konkurrenz auch dopt. Es ergibt sich eine Situation, in der für jeden Fahrer Dopen die dominante Strategie ist, obwohl es insgesamt alle vermutlich vorziehen würden, dass keiner betrügt.

Zusatzüberlegungen aufgrund von komplexer Realität

Zugegeben ist dies eine sehr vereinfachte Darstellung. So könnte man etwa bezweifeln, dass ein Fahrer sich mit Doping besser stellt als ohne, wenn die Konkurrenz nicht dopt. Er könnte etwa großen Wert auf Fairness legen und nicht mit ,,fiesen Tricks“ gewinnen wollen. Damit wäre dann Doping keine dominante Strategie mehr für ihn und man könnte dieses Spielproblem nicht mehr als Gefangenendilemma bezeichnen. Aufgrund der großen Anzahl an ,,Spielern“ bei großen Radrennen und dem offenbar großen Vorteil, den man sich durch Doping verschafft, sehen sich vermutlich diese ,,fairen Sportler“, für die Doping keine dominante Strategie ist, dazu gezwungen zu dopen, da sie sonst mit den wahrscheinlich mitfahrenden Dopern nicht mithalten können. Analog zum Ergebnis des Gefangenendilemmas können so bei einem Radrennen ausschließlich dopende Sportler teilnehmen, die alle davon ausgehen, dass einige Betrüger unter den Teilnehmern sind, denen jeder Einzelne keinen Vorteil gewähren möchte.